(実装)ガウス過程回帰を理解したい-Gaussian Process Regression

本記事ではガウス過程回帰の実装を行っていきたいと思います。

理論などのインプットばかりではわかった気にはなっても使いこなすことはできないので、本記事を通して実装をアウトプットしました。

ガウス過程回帰とは

ガウス過程回帰は入力$X$から出力$y$への関数を確率変数として推定します。ガウス過程はデータの平均値を予測すると同時に，その分散を出力します。

いま、学習データ$x_1,\cdots,x_N$に対応する出力$f(x_1),\cdots,\cdots,f(x_N)$がガウス分布に従っているとき、 新しい入力データ集合$X$に対応する出力$y$を予測したいときを考えると、その出力は次の多変量ガウス分布に従っています。

$$p(y^{\ast}|\mathbf{x}^{\ast},X,Y)=\mathcal{N}(\mathbf{k}^T_{\ast}\mathbf{K}^{-1}\mathbf{Y},\mathbf{k}_{\ast,\ast}-\mathbf{k}^T_{\ast}\mathbf{K}^{-1}\mathbf{k}_{\ast})$$

$\mathbf{k}_{\ast}$は学習データ$X$と新規のデータ$\mathbf{x}^{\ast}$のカーネル、$\mathbf{K}$は学習データ$X$と学習$X$のカーネル、$\mathbf{K}_{\ast,\ast}$は新規のデータ$\mathbf{x}^{\ast}$と新規のデータ$\mathbf{x}^{\ast}$のカーネルです．

使用データ

import numpy
np.random.seed(0)
resolution =  20
x_train = np.sort(np.random.rand(resolution) * 15)
y = np.sin(x_train) + np.random.rand(len(x_train))
x_test = np.linspace(0, 20, resolution)

$x$を$0から15$の範囲でランダムに生成して$y=sin(x)+\epsilon$の関数へ入力して学習データを作成します。$\epsilon$はガウスノイズです。 テストデータに$0から20$の範囲を等間隔で学習データ分を入力として作成します。

学習データをプロットすると次のようになります。

平均 $\mathbf{k}^T_{\ast}\mathbf{K}^{-1}\mathbf{Y}$ を求める

ガウス過程回帰では任意のカーネル関数を用います。予測される確率分布の平均$\mathbf{k}^T_{\ast}\mathbf{K}^{-1}\mathbf{Y}$にもカーネル関数があります。

ここではカーネル関数はガウス関数を用います。

$$k(\mathbf{x},\mathbf{x'}) = \exp(-\frac{\sigma}{2}||\mathbf{x}-\mathbf{x'}||^2)$$

X_X_dist = np.sqrt((x_train[:, None] - x_train[None, :]) ** 2)
K = np.exp((-0.5 * self.σ * X_X_dist))
K_inv = np.linalg.inv(K)

X_test_dist = np.sqrt((x_train[:, None] - x_test[None, :]) ** 2)
k_star = np.exp((-0.5 * self.σ * X_test_dist))

y_pred_mean = k_star.T @ K_inv @ y

分散$\mathbf{k}_{\ast,\ast}-\mathbf{k}^T_{\ast}\mathbf{K}^{-1}\mathbf{k}_{\ast}$を求める

予測される確率分布の分散$\mathbf{k}_{\ast,\ast}-\mathbf{k}^T_{\ast}\mathbf{K}^{-1}\mathbf{k}_{\ast}$にもカーネル関数があります。

ここでのカーネル関数もガウス関数を用います。

$$k(\mathbf{x},\mathbf{x'}) = \exp(-\frac{\sigma}{2}||\mathbf{x}-\mathbf{x'}||^2)$$

X_X_dist = np.sqrt((x_train[:, None] - x_train[None, :]) ** 2)
K = np.exp((-0.5 * self.σ * X_X_dist))
K_inv = np.linalg.inv(K)

X_test_dist = np.sqrt((x_train[:, None] - x_test[None, :]) ** 2)
k_star = np.exp((-0.5 * self.σ * X_test_dist))
test_test_dist = np.sqrt((x_test - x_test) ** 2)
k_star_star = np.exp((-0.5 * self.σ * test_test_dist))

y_pred_cov = k_star_star - ((k_star.T @ K_inv) @ k_star)  # 分散共分散行列
y_pred_std = np.sqrt(np.diag(y_pred_cov))

ここで$標準偏差=\sqrt{分散}$から標準偏差を求めています。

この標準偏差を求めることから、予測分布の不確かさがわかります。

実行結果

ガウス過程回帰の実装コードを描画のコードを足して Class にしてまとめました。

全体コードは次のようになります。

import numpy as np
import matplotlib.pyplot as plt

class gpr(object):
    def __init__(self, σ):
        self.σ = σ

    def fit(self, x_train, x_test, y):
        X_X_dist = np.sqrt((x_train[:, None] - x_train[None, :]) ** 2)
        K = np.exp((-0.5 * self.σ * X_X_dist))
        K_inv = np.linalg.inv(K)

        X_test_dist = np.sqrt((x_train[:, None] - x_test[None, :]) ** 2)
        k_star = np.exp((-0.5 * self.σ * X_test_dist))

        test_test_dist = np.sqrt((x_test - x_test) ** 2)
        k_star_star = np.exp((-0.5 * self.σ * test_test_dist))

        y_pred_mean = k_star.T @ K_inv @ y
        y_pred_cov = k_star_star - ((k_star.T @ K_inv) @ k_star)  # 分散共分散行列
        y_pred_std = np.sqrt(np.diag(y_pred_cov))  # 標準偏差
        return y_pred_mean, y_pred_cov, y_pred_std


if __name__ == "__main__":
    np.random.seed(0)
    resolution =  20
    x_train = np.sort(np.random.rand(resolution) * 15)
    y = np.sin(x_train) +  np.random.rand(len(x_train))

    x_test = np.linspace(0, 20, resolution)

    model = gpr(σ=1.0)
    mu, var, std = model.fit(x_train, x_test, y)

    # 描画
    fig = plt.figure(figsize=(12, 4))
    plt.cla()
    plt.scatter(x_train, y, c="black", marker="o", label="train data")
    plt.plot(x_test, mu, color="red", linewidth=1, label="mean")
    plt.fill_between(x_test, mu + std, mu - std, facecolor='green', alpha=0.2, label="confidence")
    plt.legend()
    plt.show()

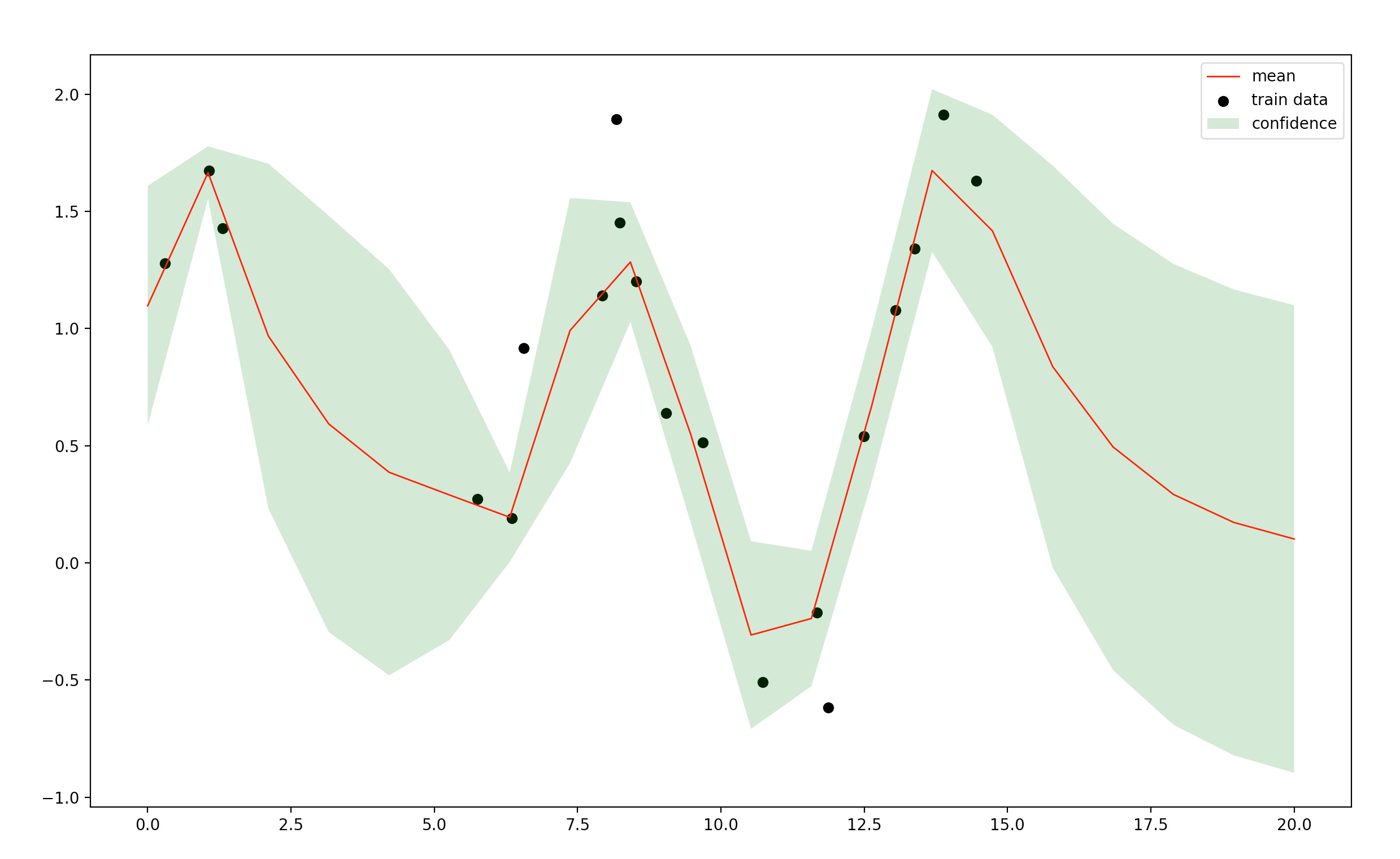
黒点は学習データです。赤い曲線が予測結果(推定したガウス分布の平均)で、緑色の領域は推定したガウス分布の共分散行列を使って計算した$2\sigma$区間を表していて、予測の信頼度が表現されています。

学習データの少ないところは分散($\sigma$の値)が大きくなっているなど、関数の不確定性まで扱えています。

このように、予測値の不確実性を出力できることはガウス過程をはじめとするベイズモデルの長所です．

終わりに

ここまで読んでくださってありがとうございます。

編集リクエストもお待ちしてます。